Your Solving the logistic growth model equation images are available. Solving the logistic growth model equation are a topic that is being searched for and liked by netizens now. You can Find and Download the Solving the logistic growth model equation files here. Find and Download all royalty-free images.
If you’re looking for solving the logistic growth model equation images information related to the solving the logistic growth model equation keyword, you have pay a visit to the right blog. Our website always provides you with hints for viewing the maximum quality video and picture content, please kindly hunt and find more informative video articles and images that match your interests.
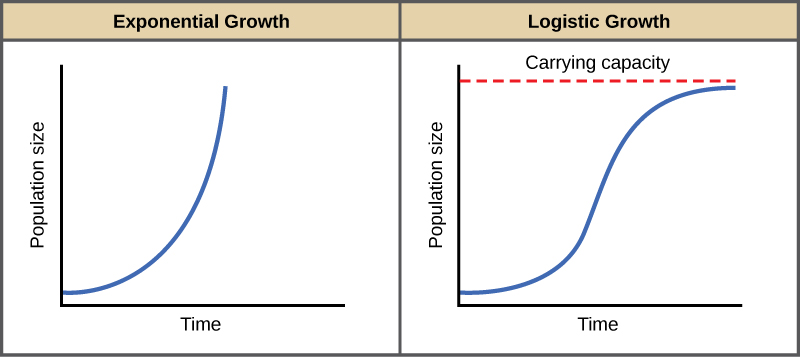
Solving The Logistic Growth Model Equation. Let ut represents the population size and t represents the time where the constant ρ 0 defines the growth rate. Multiply both sides of the equation by K and integrate. P L A e k t 1 displaystyle P frac L Ae -kt1 The above equation is the solution to the logistic growth problem with a graph of the logistic curve shown. Overview of the logistic equation.
6 5 Logistic Growth Model Years Bears Greg Kelly Hanford High School Richland Washington Ppt Download From slideplayer.com
The given data tell us that P50 K 1K 53e50k53 231 P100 K 1K 53e100k53 76. Behavior of typical solutions to the logistic equation. Hi all I need help solving the logistic growth model an ODE using Eulers Method in MATLAB. How do you solve logistic growth differential equations. Solving the Logistic Differential Equation. Thanks to all of you who support me on Patreon.
Solving the Logistic Differential Equation.
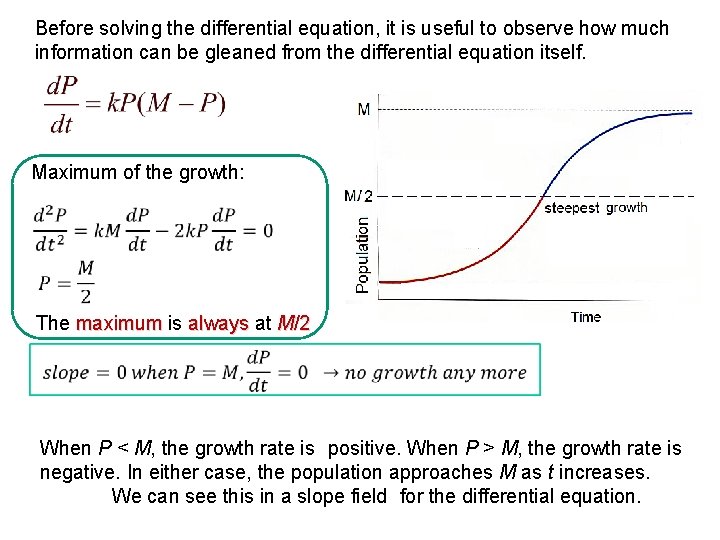
The general solution for the logistic model is. Setting the right-hand side equal to zero leads to P0 and PK as constant solutions. Thanks to all of you who support me on Patreon. Finding the general solution of the general logistic equation dNdtrN1-NK. 1 per month helps. A typical application of the Logistic equation is a common model of population growth.
Source: slideplayer.com
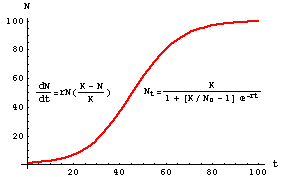
Taghavi Department of Computer Sciences Shahid Beheshti University GC Tehran Iran arXiv10082337v2 math-ph 16 Aug 2010 Abstract This paper aims to compare rational Chebyshev RC and Hermite. All solutions approach the carrying capacity as time tends to infinity at a rate depending on the intrinsic growth rate. K growth rate. Dydx ry 1- yK where r is the growth rate and K is the carrying capacity. The logistic differential equation dNdtrN1-NK describes the situation where a population grows proportionally to its size but stops growing when it reaches the size of K.
Source: youtube.com
What is K in logistic growth calculus. Solving the Logistic Differential Equation. Then the Equation 845 becomes. A typical application of the Logistic equation is a common model of population growth. What is K in logistic growth calculus.
Source: youtube.com
Here the number is the initial density of the population is the intrinsic growth rate of the population for given finite initial resources available and is the carrying capacity or maximum potential population density.
Source: youtube.com
K growth rate. Multiply both sides of the equation by K and integrate. Overview of the logistic equation. Begincases X_t1 X_t KX_t1-X_tCX_0 10 endcases Where. We can obtain K and k from these system of two equations but we are told that k 0031476 so we only need to obtain K the carrying capacity from one of the equations say the first one.
Source: calcworkshop.com
P L A e k t 1 displaystyle P frac L Ae -kt1 The above equation is the solution to the logistic growth problem with a graph of the logistic curve shown. Setting the right-hand side equal to zero leads to P0 and PK as constant solutions. Then multiply both sides by dt and divide both sides by PKP. Setting the right-hand side equal to zero leads to P0 and PK as constant solutions. The logistic differential equation is an autonomous differential equation so we can use separation of variables to find the general solution as we just did in.
Source: youtube.com
Then multiply both sides by dt and divide both sides by PKP. Finding the general solution of the general logistic equation dNdtrN1-NK. Where P is the Population Size N is often used instead t is Time r is the Growth Rate K is the Carrying Capacity. Setting the right-hand side equal to zero leads to P0 and PK as constant solutions. We can obtain K and k from these system of two equations but we are told that k 0031476 so we only need to obtain K the carrying capacity from one of the equations say the first one.
Source: slidetodoc.com
If youre seeing this message it means were having trouble loading external resources on our website. And the logistic growth got its equation. Then multiply both sides by dt and divide both sides by PKP. P n P n1 r1 P n1 KP n1 P n P n 1 r 1 P n 1 K P n 1. The given data tell us that P50 K 1K 53e50k53 231 P100 K 1K 53e100k53 76.
Source: slideplayer.com
If youre seeing this message it means were having trouble loading external resources on our website. The first solution indicates that when there are no organisms present the. Then multiply both sides by dt and divide both sides by PKP. K growth rate. For those situations we can use a continuous logistic model in the form.
Source: geogebra.org
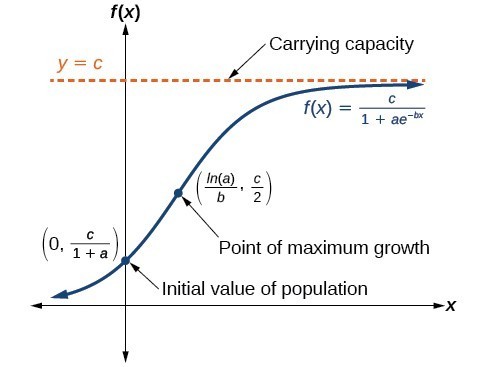
Overview of the logistic equation. Where t t stands for time in years c c is the carrying capacity the maximal population P 0 P 0 represents the starting quantity and r r is the rate of growth. Begincases X_t1 X_t KX_t1-X_tCX_0 10 endcases Where. Solving the Logistic Differential Equation. X_n The population at a given time.
Source: courses.lumenlearning.com
Begincases X_t1 X_t KX_t1-X_tCX_0 10 endcases Where. The Logistic Equation and. If youre seeing this message it means were having trouble loading external resources on our website. That the exponential growth model doesnt fit well. Finding the general solution of the general logistic equation dNdtrN1-NK.
Source: condellpark.com
Solution of the Logistic Equation. The given data tell us that P50 K 1K 53e50k53 231 P100 K 1K 53e100k53 76. Numerical approximations for population growth model by Rational Chebyshev and Hermite Functions collocation approach. Dydx ry 1- yK where r is the growth rate and K is the carrying capacity. Overview of the logistic equation.
Source: uwyo.edu
Instead we may assume a logistic growth model and find the carrying capacity based on the data provided. That the exponential growth model doesnt fit well. All solutions approach the carrying capacity as time tends to infinity at a rate depending on the intrinsic growth rate. Begincases X_t1 X_t KX_t1-X_tCX_0 10 endcases Where. The solution is kind of hairy but its worth bearing with us.
Source: nagwa.com
The general solution for the logistic model is. The general solution for the logistic model is. A typical application of the Logistic equation is a common model of population growth. That the exponential growth model doesnt fit well. Solution of the Logistic Equation.
Source: cochranmath.pbworks.com
Taghavi Department of Computer Sciences Shahid Beheshti University GC Tehran Iran arXiv10082337v2 math-ph 16 Aug 2010 Abstract This paper aims to compare rational Chebyshev RC and Hermite. Find exponential equations using graphs solve exponential growth and decay problems use logistic growth models Example 1. Instead we may assume a logistic growth model and find the carrying capacity based on the data provided. That the exponential growth model doesnt fit well. The graph of g is the transformation of f x.
Source: slidetodoc.com
The Logistic Equation and. P n P n1 r1 P n1 KP n1 P n P n 1 r 1 P n 1 K P n 1. Solution of the Logistic Equation. The virtue of having a single first-order equation representing yeast dynamics is that we can solve this equation using integration techniques. Then the Equation 845 becomes.
Source: math.stackexchange.com
The general solution for the logistic model is. That the exponential growth model doesnt fit well. Solving the Logistic Differential Equation. Hi all I need help solving the logistic growth model an ODE using Eulers Method in MATLAB. Setting the right-hand side equal to zero leads to P0 and PK as constant solutions.
Source: youtube.com
And the logistic growth got its equation. Solution of the Logistic Equation. The virtue of having a single first-order equation representing yeast dynamics is that we can solve this equation using integration techniques. You da real mvps. Another application of Logistic curve is in medicine where the Logistic differential equation is used to model the growth of tumors.
Source: medium.com
The virtue of having a single first-order equation representing yeast dynamics is that we can solve this equation using integration techniques. Taghavi Department of Computer Sciences Shahid Beheshti University GC Tehran Iran arXiv10082337v2 math-ph 16 Aug 2010 Abstract This paper aims to compare rational Chebyshev RC and Hermite. Let ut represents the population size and t represents the time where the constant ρ 0 defines the growth rate. 42 Applications of Exponential Functions In this section you will learn to. For those situations we can use a continuous logistic model in the form.
This site is an open community for users to share their favorite wallpapers on the internet, all images or pictures in this website are for personal wallpaper use only, it is stricly prohibited to use this wallpaper for commercial purposes, if you are the author and find this image is shared without your permission, please kindly raise a DMCA report to Us.
If you find this site serviceableness, please support us by sharing this posts to your preference social media accounts like Facebook, Instagram and so on or you can also bookmark this blog page with the title solving the logistic growth model equation by using Ctrl + D for devices a laptop with a Windows operating system or Command + D for laptops with an Apple operating system. If you use a smartphone, you can also use the drawer menu of the browser you are using. Whether it’s a Windows, Mac, iOS or Android operating system, you will still be able to bookmark this website.
