Your Population growth differential equation calculator images are ready. Population growth differential equation calculator are a topic that is being searched for and liked by netizens today. You can Get the Population growth differential equation calculator files here. Download all royalty-free photos.
If you’re looking for population growth differential equation calculator images information linked to the population growth differential equation calculator keyword, you have come to the ideal blog. Our website frequently provides you with hints for viewing the highest quality video and image content, please kindly search and find more informative video articles and images that match your interests.
Population Growth Differential Equation Calculator. There is a substantial number of processes for which you can use this exponential growth calculator. POPULATION GROWTH MODELS A simple expression that incorporates both assumptions is given by the equation If P is small compared with K then PK is close to 0. In this video I prove that the growth rate in a population assuming it uses the logistic model is fastest at half the carrying capacity. Dt dpdt kp dt.
Population Growth From math24.net
We derive this equation to calculate the population at any point as follow. We consider here a few models of population growth proposed by economists and physicists. I manually did each years population to get to the next year. The Logistic Growth calculator computes the logistic growth based on the per capita growth rate of population population size and carrying capacity. P t P o k T Where P t is population at time t. 210000 leave the city per year.
I manually did each years population to get to the next year.
The simplest yet incomplete model is modeled by the rate of growth being equal to the size of the population. How do you calculate logistic population growth. A way that we can set up a differential equations for population growth is with the formula. A quantitygrows linearly if it grows by a constant amount for each unit of time. The population of a species that grows exponentially over time can be modeled by PtPekt where Pt is the population after time t P is the original population when t0 and k is the growth constant. As the logistic equation is a separable differential equation the population may be solved explicitly by the shown formula.
Source: geogebra.org
This model reflects exponential. 3 Single Species Population Models 31 Exponential Growth We just need one population variable in this case. Dpdt kp dp reperesents the population and how much its growing. How do you calculate logistic population growth. Equation for Logistic Population Growth.
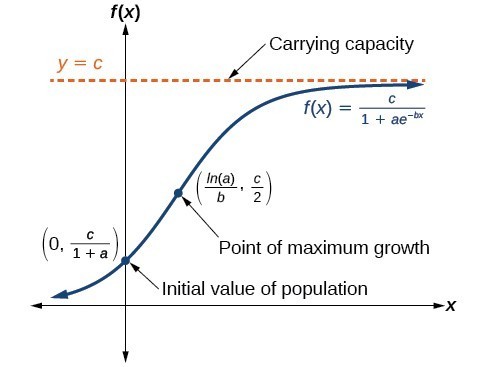Source: courses.lumenlearning.com
3 Single Species Population Models 31 Exponential Growth We just need one population variable in this case. Dt dpdt kp dt. What is the population in 1910. K the relative growth rate. A differential equation of the separable class.
Source: scirp.org
As the logistic equation is a separable differential equation the population may be solved explicitly by the shown formula. The calculator returns the logistic growth rate in growth per day. K is constant growth rate. The constant solutions are P0 and PM. P o is population at time zero.
Source: chegg.com
As the logistic equation is a separable differential equation the population may be solved explicitly by the shown formula. We consider here a few models of population growth proposed by economists and physicists. Xt x 0 1 r100 t. The net growth rate at that time would have been around 231 per year. A way that we can set up a differential equations for population growth is with the formula.
Source: pinterest.com
Clearly when P is small compared to M the equation reduces to the exponential one. This model reflects exponential. DP dt kP with P0 P 0 We can integrate. P1 PK k dt. The net growth rate at that time would have been around 231 per year.
Source: zo.utexas.edu
Is used when there is a quantity with an initial value x 0 that changes over time t with a constant rate of change rThe exponential function appearing in the above formula has a. The difference between the birth rate and death rate is 16. Linear Population Growth. It is possible to construct an exponential growth model of population which begins with the assumption that the rate of population growth is proportional to the current population. So dP dt 0 1 dP P kP dt K POPULATION GROWTH MODELS Equation 2 Equation 2 is called the logistic differential equation.
Source: khanacademy.org
A way that we can set up a differential equations for population growth is with the formula. So dP dt 0 1 dP P kP dt K POPULATION GROWTH MODELS Equation 2 Equation 2 is called the logistic differential equation. So you will grow by 60 bunnies per year and then you would shrink by the 15 that died. Clearly when P is small compared to M the equation reduces to the exponential one. Linear Population Growth.
Source: math24.net
The population of a species that grows exponentially over time can be modeled by PtPekt where Pt is the population after time t P is the original population when t0 and k is the growth constant. Is used when there is a quantity with an initial value x 0 that changes over time t with a constant rate of change rThe exponential function appearing in the above formula has a. T is elapsed time in years from time zero. A quantitygrows linearly if it grows by a constant amount for each unit of time. The growth of the population was very close to exponential.
Source: uctsc.org
Dpp kpp dt. A differential equation of the separable class. This differential equation. DP dt kP 1 P K. As time goes on the two graphs separate.
Source: pinterest.com
Choose units and enter the following. DP dt kP with P0 P 0 We can integrate. The calculator returns the logistic growth rate in growth per day. A differential equation of the separable class. This model reflects exponential.
Source: chegg.com
P size of the population with respect to time. The general rule of thumb is that the exponential growth formula. I manually did each years population to get to the next year. Logistic Equation for Model Population Growth A model for population growth which attempts to take into consideration the fact that as a population grows resources become limited resulting in a slowing of the growth rate is given by the following differential equation. Population growth is a dynamic process that can be effectively described using differential equations.
Source: epythonguru.com
Well your population growth rate if you think about just even say a given year in that year youll grow your population by 60 bunnies per year. There is a substantial number of processes for which you can use this exponential growth calculator. We will let Nt be the number of individuals in a population at time t. P in 1901 80000001016-210000 7918000. Is used when there is a quantity with an initial value x 0 that changes over time t with a constant rate of change rThe exponential function appearing in the above formula has a.
Source: math24.net
So dP dt kP If P K then 1 PK is negative.
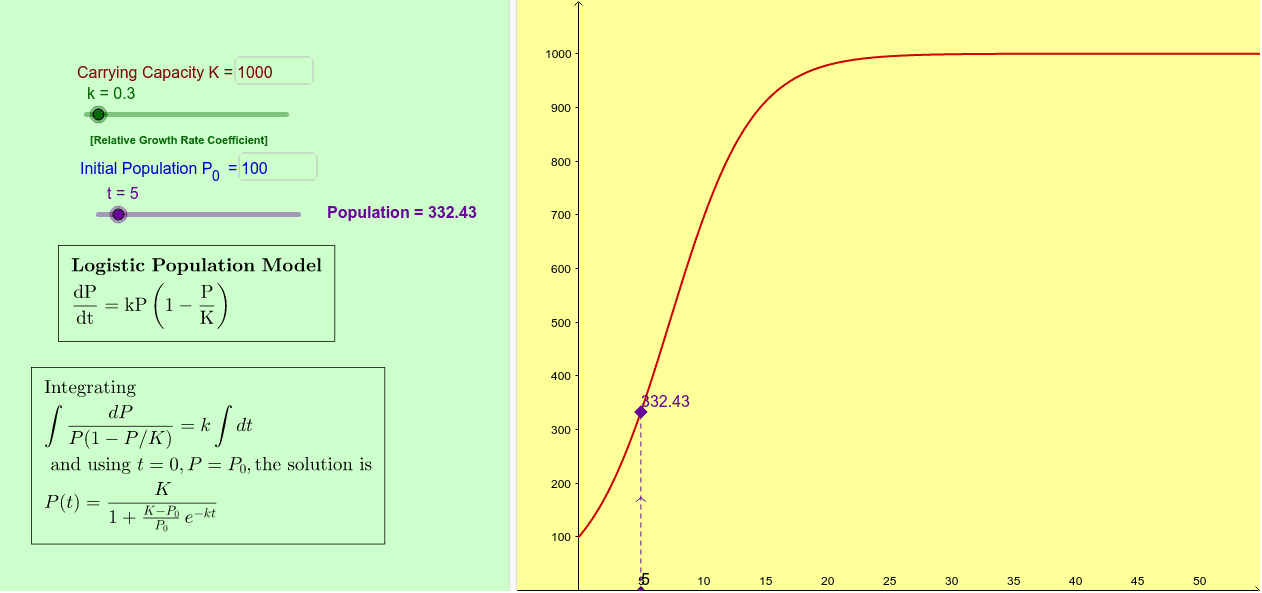Source: geogebra.org
As the logistic equation is a separable differential equation the population may be solved explicitly by the shown formula. The simplest yet incomplete model is modeled by the rate of growth being equal to the size of the population. Equation for Logistic Population Growth. We will let Nt be the number of individuals in a population at time t. 210000 leave the city per year.
Source: calcworkshop.com
The corre- sponding equation is the so called logistic differential equation. POPULATION GROWTH MODELS A simple expression that incorporates both assumptions is given by the equation If P is small compared with K then PK is close to 0. So you will grow by 60 bunnies per year and then you would shrink by the 15 that died. DP dt kP 1 P K. This happens because the population increases and the logistic differential equation states that the growth rate decreases as the population increases.
Source: math24.net
Differential equations differential to the Solutions Predictions about the system behaviour Model Figure 93. 210000 leave the city per year. The constant solutions are P0 and PM. I prove this using. As time goes on the two graphs separate.
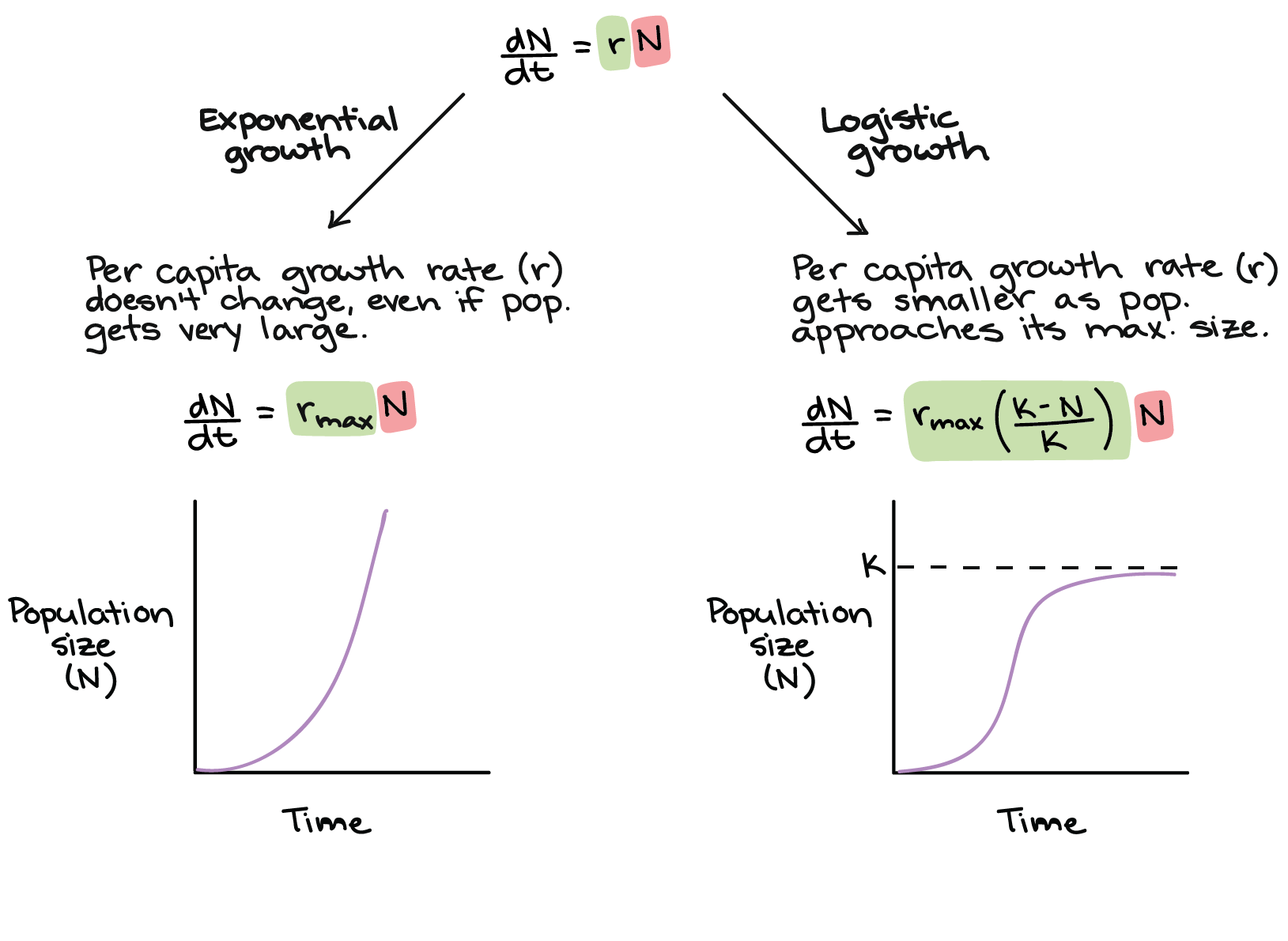Source: khanacademy.org
The general rule of thumb is that the exponential growth formula. Differential equations differential to the Solutions Predictions about the system behaviour Model Figure 93. So dP dt 0 1 dP P kP dt K POPULATION GROWTH MODELS Equation 2 Equation 2 is called the logistic differential equation. It is possible to construct an exponential growth model of population which begins with the assumption that the rate of population growth is proportional to the current population. A quantitygrows linearly if it grows by a constant amount for each unit of time.
Source: uctsc.org
Dt dpdt kp dt. Dpp kpp dt. P in 1901 80000001016-210000 7918000. As time goes on the two graphs separate. What is the population in 1910.
This site is an open community for users to submit their favorite wallpapers on the internet, all images or pictures in this website are for personal wallpaper use only, it is stricly prohibited to use this wallpaper for commercial purposes, if you are the author and find this image is shared without your permission, please kindly raise a DMCA report to Us.
If you find this site serviceableness, please support us by sharing this posts to your favorite social media accounts like Facebook, Instagram and so on or you can also save this blog page with the title population growth differential equation calculator by using Ctrl + D for devices a laptop with a Windows operating system or Command + D for laptops with an Apple operating system. If you use a smartphone, you can also use the drawer menu of the browser you are using. Whether it’s a Windows, Mac, iOS or Android operating system, you will still be able to bookmark this website.
