Your Exponential function mean value theorem images are ready in this website. Exponential function mean value theorem are a topic that is being searched for and liked by netizens now. You can Get the Exponential function mean value theorem files here. Find and Download all royalty-free images.
If you’re looking for exponential function mean value theorem images information linked to the exponential function mean value theorem keyword, you have visit the right blog. Our website always gives you hints for downloading the maximum quality video and picture content, please kindly hunt and locate more informative video content and graphics that match your interests.
Exponential Function Mean Value Theorem. Let pt denote the distance in meters to the right of the origin of a particle at time tminutes after noon. Students will be able to. Try to find the value of c before reading further. By Taylors Theorem we have for n a fixed positive integer.
Chapter 4 Applications Of Derivatives Section 4 2 Mean Value Theorem Ppt Download From slideplayer.com
Let pt denote the distance in meters to the right of the origin of a particle at time tminutes after noon. Therefore the conditions for the Mean Value Theorem. Understand how Rolles theorem relates to the mean value theorem understand the mean value theorem and when its conditions are satisfied find points in an interval that satisfy the mean value theorem for a given function. Find the values guaranteed by Rolles Theorem or the Mean Value Theorem. If f is a function that is continuous on the closed interval a b and differentiable on the open interval a b then there is a point c in a b such that f. We solve it in steps.
Roughly speaking the Extreme Value Theorem says that there has to be a maximum and a minimum.
V c s. We can now answer our second question above. This is the Mean Value Theorem with f x e x a 1 and b 3. We look for c. For this function there are two values and such that the tangent line to. F a f b 0 f a f b 0.
Source: slideplayer.com
V c s c s 1 s 0 1 0 45 mph. The approximation of the exponential function by polynomial using Taylors or Maclaurins formula Properties of the power series expansion of the exponential function. If f is a function that is continuous on the closed interval a b and differentiable on the open interval a b then there is a point c in a b such that f. For some a. If its in the interior Fermats Theorem says that it has to be a critical point.
Source: sciencedirect.com
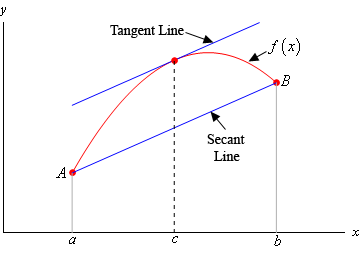
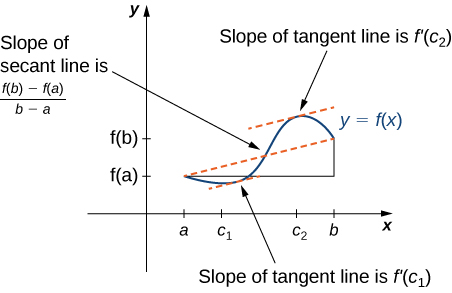
Determine whether Rolles Theorem or the Mean Value Theorem can be applied. Sketch pictures to illustrate why the Mean Value Theorem is true. About Press Copyright Contact us Creators Advertise Developers Terms Privacy Policy Safety How YouTube works Test new features Press Copyright Contact us Creators. Mean Value Theorem Suppose that f f has a derivative on the interval ab a b and is continuous on the interval ab a b. Try to find the value of c before reading further.
Source: m.youtube.com
Like we did in the previous proof we can pick any x 1 x 2 a b such that x 1 x 2. We look for c. By Taylors Theorem we have for n a fixed positive integer. Since f is differentiable on the interior it has to be a point where fc0. C 0 1 c 0 1 the speed of the car was exactly.
Source: youtube.com
Try to find the value of c before reading further. Determine whether Rolles Theorem or the Mean Value Theorem can be applied. After completing this section students should be able to do the following. Assuming that the position function. The Exponential Function e x Taking our definition of e as the infinite n limit of 1 1 n n it is clear that e x is the infinite n limit of 1 1 n n x.
Source: nagwa.com
The approximation of the exponential function by polynomial using Taylors or Maclaurins formula Properties of the power series expansion of the exponential function. This theorem is used to prove statements about a function on an interval starting from local hypotheses about. V c s. Mean Value Theorem Suppose that f f has a derivative on the interval ab a b and is continuous on the interval ab a b. By Taylors Theorem we have for n a fixed positive integer.
Source: nagwa.com
For this function there are two values and such that the tangent line to. Understand the statement of the Extreme Value Theorem. Like we did in the previous proof we can pick any x 1 x 2 a b such that x 1 x 2. After completing this section students should be able to do the following. We compute f b f a b a e 3 e 2.
Source: tutorial.math.lamar.edu
The approximation of the exponential function by polynomial using Taylors or Maclaurins formula Properties of the power series expansion of the exponential function. Try to find the value of c before reading further. C fbfa ba f c f b f a b a. The x -value of this point is the c in the MVT. Students will be able to.
Source: khanacademy.org
We derive the derivative of the natural exponential function. We look for c. Mean Value Theorem Suppose that f f has a derivative on the interval ab a b and is continuous on the interval ab a b. V c s. Since f is differentiable on the interior it has to be a point where fc0.
Source: opentextbc.ca
After completing this section students should be able to do the following. The Exponential Function e x Taking our definition of e as the infinite n limit of 1 1 n n it is clear that e x is the infinite n limit of 1 1 n n x. That means we can use the Mean Value Theorem. Try to find the value of c before reading further. The approximation of the exponential function by polynomial using Taylors or Maclaurins formula Properties of the power series expansion of the exponential function.
Source: sfu.ca
This in turn means that the sum is also continuous and differentiable everywhere and so the function will be continuous on left - 23 right and differentiable on left - 23 right. F a f b 0 f a f b 0. Sketch pictures to illustrate why the Mean Value Theorem is true. Assuming that the position function. A x 1 x 2 b.
Source: sciencedirect.com
This theorem is used to prove statements about a function on an interval starting from local hypotheses about. V c s c s 1 s 0 1 0 45 mph. F a f b 0 f a f b 0. Use this information to guess a value for the instantaneous velocity of particle at 1202pm. Try to find the value of c before reading further.
Source: matheno.com
Understand the statement of the Mean Value Theorem. For some a. The x -value of this point is the c in the MVT. After completing this section students should be able to do the following. 0 t 1 h.
Source: cliffsnotes.com
This is the Mean Value Theorem with f x e x a 1 and b 3. Like we did in the previous proof we can pick any x 1 x 2 a b such that x 1 x 2. If pt pt t345t give the average velocity on the intervals 221 and 2201. It is one of the most important results in real analysis. For this function there are two values and such that the tangent line to.
Source: khanacademy.org
Assuming that the position function. Next because f x f x is a polynomial it is continuous and differentiable everywhere and so we could use Rolles Theorem to see that there must be a real value c c so that f c 0 f c 0. The function is a sum of a polynomial and an exponential function both of which are continuous and differentiable everywhere. Try to find the value of c before reading further. If pt pt t345t give the average velocity on the intervals 221 and 2201.
Source: bishsoft.org
The function is a sum of a polynomial and an exponential function both of which are continuous and differentiable everywhere. The Exponential Function e x Taking our definition of e as the infinite n limit of 1 1 n n it is clear that e x is the infinite n limit of 1 1 n n x. If f is a function that is continuous on the closed interval a b and differentiable on the open interval a b then there is a point c in a b such that f. The Mean Value Theorem for Integrals If fleft x right is a continuous function on left ab right then there is a number c in left ab right such that int_abfleft x rightdx fleft c rightleft b - a right. S t s t is differentiable we can apply the Mean Value Theorem to conclude that at some time.
Source: slideplayer.com
For some a. 0 t 1 h. We can now answer our second question above. We compute f b f a b a e 3 e 2. Use this information to guess a value for the instantaneous velocity of particle at 1202pm.
Source: youtube.com
We look for c. We look for c. Mean Value Theorem Suppose that f f has a derivative on the interval ab a b and is continuous on the interval ab a b. After completing this section students should be able to do the following. Limits of Piece-wise Functions The Squeeze Theorem Continuity and the Intermediate Value Theorem Definition of continuity Continuity and piece-wise functions Continuity properties Types of discontinuities The Intermediate Value Theorem Summary of using continuity to evaluate limits Limits at Infinity Limits at infinity and horizontal asymptotes.
Source: opentextbc.ca
We derive the derivative of the natural exponential function. Next because f x f x is a polynomial it is continuous and differentiable everywhere and so we could use Rolles Theorem to see that there must be a real value c c so that f c 0 f c 0. Try to find the value of c before reading further. For this function there are two values and such that the tangent line to. Taylors theorem Taylors formula - The extended mean value theorem.
This site is an open community for users to do sharing their favorite wallpapers on the internet, all images or pictures in this website are for personal wallpaper use only, it is stricly prohibited to use this wallpaper for commercial purposes, if you are the author and find this image is shared without your permission, please kindly raise a DMCA report to Us.
If you find this site helpful, please support us by sharing this posts to your favorite social media accounts like Facebook, Instagram and so on or you can also save this blog page with the title exponential function mean value theorem by using Ctrl + D for devices a laptop with a Windows operating system or Command + D for laptops with an Apple operating system. If you use a smartphone, you can also use the drawer menu of the browser you are using. Whether it’s a Windows, Mac, iOS or Android operating system, you will still be able to bookmark this website.
