Your Exponential formula for population growth images are available. Exponential formula for population growth are a topic that is being searched for and liked by netizens today. You can Find and Download the Exponential formula for population growth files here. Download all royalty-free images.
If you’re searching for exponential formula for population growth pictures information connected with to the exponential formula for population growth keyword, you have come to the right site. Our website frequently provides you with suggestions for downloading the maximum quality video and image content, please kindly surf and find more enlightening video content and graphics that fit your interests.
Exponential Formula For Population Growth. B b is the growth factor. Y a 1 r x. That is a quantity that grows or decays in proportion to itself per unit of input. The exponential function appearing in the above formula has a base equal to 1 r100.
How Do You Calculate Population Growth Example From socratic.org
A P 0 a P 0 is the initial value or principal value of P. For any real number x and any positive real numbers a and b such that. This Equation involves the exponents of Rate x Time and this is why Exponential patterns of increase in Populations occur. In 2005 there were 180 inhabitants in a remote town. The general rule of thumb is that the exponential growth formula. Formula of Exponential Growth.
Y a 1 r x.
EqC frac x_. Using the given information we have to find the constant λ to complete the formula. Where y t value at time t. Lets ignore the decimal part since its not a full person. Exponential growth is modeled an exponential equation. The general formula used to represent population growth is where represents the initial population r is the population growth rate t is the elapsed time and f is the period over which the population grows by a rate of r.
Source: kristakingmath.com
Decay exponentially at least for a while. A0 initial value amount before measuring growth or decay e exponential e 271828183. R the growth rate. K 0 the amount is decreasing decaying t time that has passed. When we have continuous population growth we can model the population with the general formula where represents the initial population λ is the exponential growth constant and t is time.
Source: socratic.org
X number of time intervals passed days months years y amount after x time. Formula of Exponential Growth. With a growth rate of approximately 168 what was the population in 1955. Where eqP_0 eq is the starting value or starting population hence P eqr eq is the rate of growth and eqt eq is the unit of time over which growth is. R growth rate as a decimal.
Source: slidetodoc.com
X t x 0 1 r100 t. R the growth rate. But sometimes things can grow or the opposite. P t 1003t P t 100 3 t. Formula of Exponential Growth.
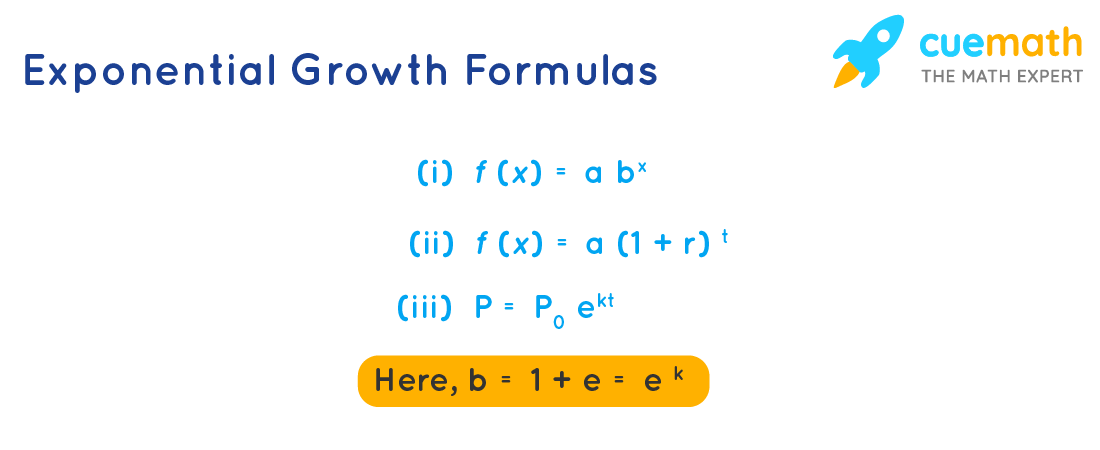Source: cuemath.com
K continuous growth rate also called constant of proportionality k 0 the amount is increasing growing. It shows up in short-run population growth among people and animals interest earned in banking. EqC frac x_. Ekt P 0. In 1950 the worlds population was 2555982611.
Source: openalgebra.com
K rate of growth when 0 or decay when. X number of time intervals passed days months years y amount after x time. Where eqP_0 eq is the starting value or starting population hence P eqr eq is the rate of growth and eqt eq is the unit of time over which growth is. Formula of Exponential Growth. So a 100 a 100 and b 3.
Source: socratic.org
EqC frac x_. R growth rate as a decimal. Exponential equations to model population growth. The Exponential Equation is a Standard Model Describing the Growth of a Single Population. Exponential growth is when a pattern of data increases with passing time by forming a curve of exponential growth.
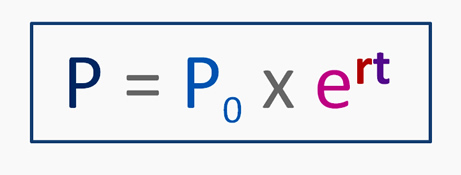Source: passyworldofmathematics.com
So our guess is that the worlds population in 1955 was 2779960539. A value at the start. X number of time intervals passed days months years y amount after x time. For the bacteria population we have. Exponential growth produces a J-shaped curve.
Source: onlinemathlearning.com
When we have continuous population growth we can model the population with the general formula where represents the initial population λ is the exponential growth constant and t is time. This is an example of exponential growth. P t P0 ert. Eulers number e is shorthand for the exponential function where P 0. Exponential growth is when a pattern of data increases with passing time by forming a curve of exponential growth.
Source: youtube.com
The population of a species that grows exponentially over time can be modeled by. So we have a generally useful formula. X number of time intervals passed days months years y amount after x time. Exponential growth is modeled an exponential equation. X t x 0 1 r100 t.
Source: math-faq.com
Exponential equations to model population growth. This formula is used to express a function of exponential growth. R growth rate as a decimal. Is used when there is a quantity with an initial value x 0 that changes over time t with a constant rate of change r. X t x 0 1 r100 t.
Source: omnicalculator.com
Where eqP_0 eq is the starting value or starting population hence P eqr eq is the rate of growth and eqt eq is the unit of time over which growth is. In 1950 the worlds population was 2555982611. R growth rate as a decimal. X t x 0 1 r100 t. The population of a species that grows exponentially over time can be modeled by.
Source: slideplayer.com
Exponential growth is modeled an exponential equation. Ekt P 0. Exponential growth is when a pattern of data increases with passing time by forming a curve of exponential growth. X t x 0 1 r100 t. P t abt P t a b t.
Source: coolmath.com
B b is the growth factor. Using the given information we have to find the constant λ to complete the formula. P t 1003t P t 100 3 t. Formula for exponential growth is X t X0 ert. Lets ignore the decimal part since its not a full person.
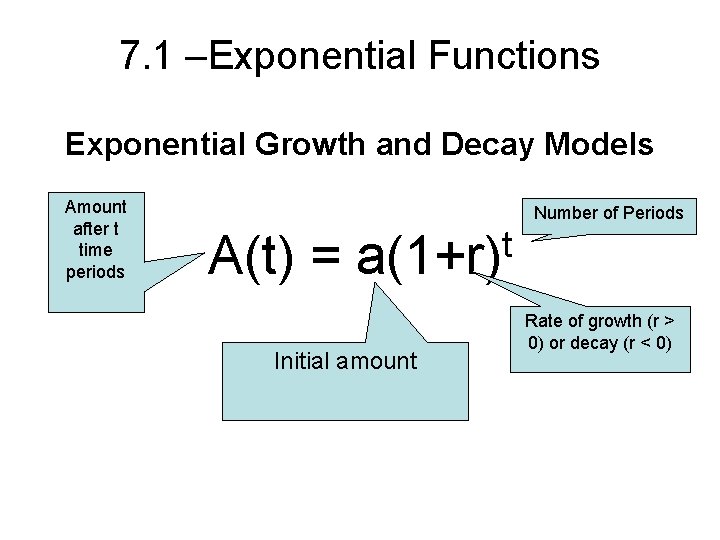Source: slidetodoc.com
In 1950 the worlds population was 2555982611. This formula is used to express a function of exponential growth. Image Copyright 2013 by Passys World of Mathematics. Exponential Population Growth Equation - 9 images - lesson 15 exponential growth and decay solow swan model with population growth part 1 of 2. Is used when there is a quantity with an initial value x 0 that changes over time t with a constant rate of change rThe exponential function appearing in the above formula has a base equal to 1.
Source: m.youtube.com
Its represented by the equation. A value at the start. Exponential growth is modeled an exponential equation. P t 1003t P t 100 3 t. For the bacteria population we have.
Source: youtube.com
K 0 the amount is decreasing decaying t time that has passed. But sometimes things can grow or the opposite. The general rule of thumb is that the exponential growth formula. That is a quantity that grows or decays in proportion to itself per unit of input. It shows up in short-run population growth among people and animals interest earned in banking.
Source: youtube.com
This Equation involves the exponents of Rate x Time and this is why Exponential patterns of increase in Populations occur. Y t a e kt. EqC frac x_. Is used when there is a quantity with an initial value x 0 that changes over time t with a constant rate of change r. A value at the start.
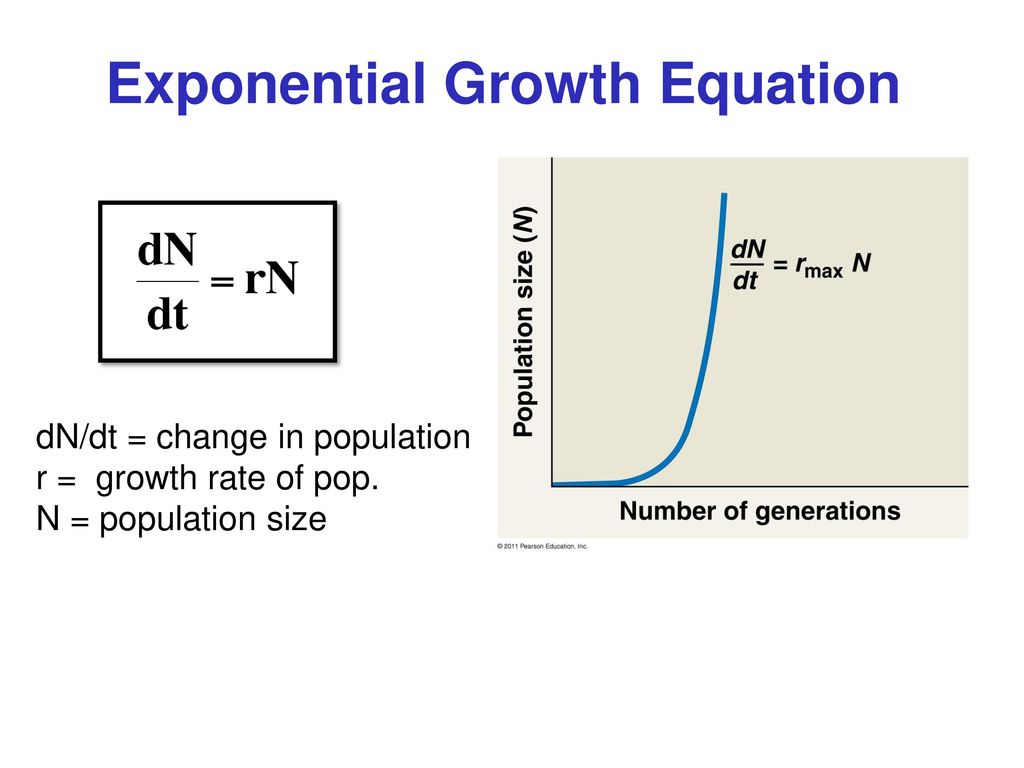Source: slideplayer.com
EqGr frac P_ 2 - P_ 1 t eq Percent change in growth. Where y t value at time t. P t abt P t a b t. Exponential equations to model population growth. K rate of growth when 0 or decay when.
This site is an open community for users to do sharing their favorite wallpapers on the internet, all images or pictures in this website are for personal wallpaper use only, it is stricly prohibited to use this wallpaper for commercial purposes, if you are the author and find this image is shared without your permission, please kindly raise a DMCA report to Us.
If you find this site convienient, please support us by sharing this posts to your preference social media accounts like Facebook, Instagram and so on or you can also save this blog page with the title exponential formula for population growth by using Ctrl + D for devices a laptop with a Windows operating system or Command + D for laptops with an Apple operating system. If you use a smartphone, you can also use the drawer menu of the browser you are using. Whether it’s a Windows, Mac, iOS or Android operating system, you will still be able to bookmark this website.
