Your Expenditure minimization definition images are available in this site. Expenditure minimization definition are a topic that is being searched for and liked by netizens now. You can Find and Download the Expenditure minimization definition files here. Get all royalty-free photos and vectors.
If you’re searching for expenditure minimization definition pictures information linked to the expenditure minimization definition keyword, you have pay a visit to the ideal site. Our website always provides you with hints for seeking the maximum quality video and image content, please kindly surf and locate more informative video content and graphics that match your interests.
Expenditure Minimization Definition. The process of converting a finite-state machine to an equivalent minimal machine. The consumption bundles that minimize expenditure provided the constraints of the two problems fimatch upfl. The chapter ends with a restatement of the duality results from cost minimizationhomogeneity concavity and monotonicity and the existence of a zero utility. Cost minimization is the process of reducing expenditures on unnecessary or inefficient processes.
Chapter 4 Utility Maximization And Choice Consumer Behavior From slidetodoc.com
Scale Invariant in Prices Nonincreasing in Own Price Identities Linking the Marshallian and Hicksian Demand Functions Examples. The plastic energy density and the fracture energy density. Let the budget correspondence be p 1 x p 2 y w where w is the income level. 73 Long-Run Cost Minimization. The definition of the dual kinetic potential and the constitutive restrictions into the total potential to obtain The thermodynamic equations of state can then be derived by. The chapter ends with a restatement of the duality results from cost minimizationhomogeneity concavity and monotonicity and the existence of a zero utility.
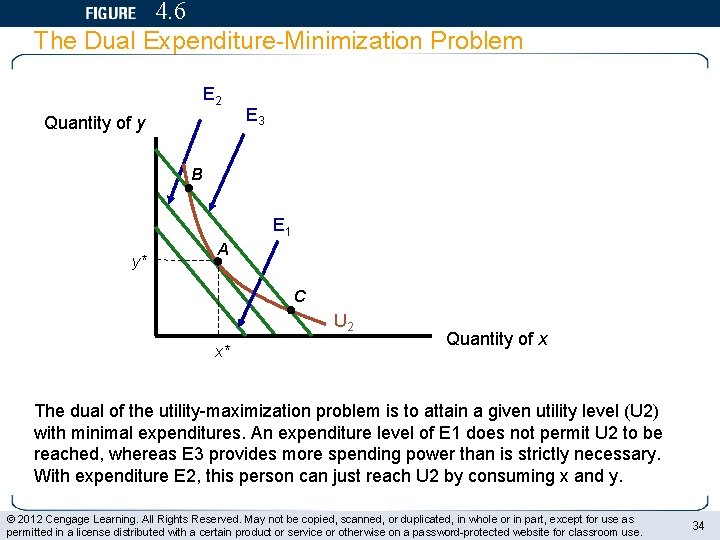
The money the agent must spend in order to attain her target utility is called her expenditure.
The utility level for the constraint in the expenditure minimization problem must be v ux where x 2x pv. Solution define an expenditure function and expenditure minimizing demand functions which behave in many respects like the usual expenditure function and compensated demand functions of the transitive consumer. The plastic energy density and the fracture energy density. 1 2 0 1 1 2 2 1 2. The index row of the third optimum solution simplex tableau see contribution margin maximization example shows the shadow prices in the slack variable columns which is the location for both and constraints while the artificial variable column is used for the constraint with the m value ignored. Cost minimization strategy and efforts can occur in any area of a business including manufacturing.
Source: slidetodoc.com
Cost minimization is the process of reducing expenditures on unnecessary or inefficient processes. The chapter ends with a restatement of the duality results from cost minimizationhomogeneity concavity and monotonicity and the existence of a zero utility. Spring 2001 Econ 11–Lecture 7 12 Calculating Hicksian Demand II Suppose U 0 Ux 1 x 2 is a utility function at a given utility level U 0 Prices are p 1 and p 2. The utility level for the constraint in the expenditure minimization problem must be v ux where x 2x pv. Ekp 1 kp 2u kp 1 h 1 p 1 p 2u kp 2 h 2 p 1 p 2u k p 1 h 1 p 1 p 2 2 1 2.
Source: slidetodoc.com
Disbursement expense income should exceed expenditures. 73 Long-Run Cost Minimization. We know that for U x y m i n x y optimalilty occurs at the point where x y. Disbursement expense income should exceed expenditures. The Lagrangian method wouldnt be of any use because Leontief function is not differentiable at the point of optimalitykink.
Source: slideplayer.com
The minimized expenditure function of this problem is given by substituting the optimal values of q i into Pq. Spring 2001 Econ 11–Lecture 7 12 Calculating Hicksian Demand II Suppose U 0 Ux 1 x 2 is a utility function at a given utility level U 0 Prices are p 1 and p 2. Formally if there is a utility function that describes preferences over n commodities the expenditure function. Describe the solution to the cost minimization problem in the long run. These changes in spending can be slight or drastic but any level of reduction in costs will likely have a dramatic effect on maximizing profits.
Source: slidetodoc.com
Total expenditures are p 1 x 1 p 2 x 2 The expenditure minimization problem is. H 1 p 1p 2u h 1 kp 1kp 2u h 2 p 1p 2u h 2 kp 1kp 2u. The index row of the third optimum solution simplex tableau see contribution margin maximization example shows the shadow prices in the slack variable columns which is the location for both and constraints while the artificial variable column is used for the constraint with the m value ignored. In the study of effective computability the process of defining a new function by searching for values of a given function using the minimization operator or μ- operator. The definition of the dual kinetic potential and the constitutive restrictions into the total potential to obtain The thermodynamic equations of state can then be derived by.
Source: slideplayer.com
1 2 0 1 1 2 2 1 2. The index row of the third optimum solution simplex tableau see contribution margin maximization example shows the shadow prices in the slack variable columns which is the location for both and constraints while the artificial variable column is used for the constraint with the m value ignored. The minimum cost for a consumer of achieving a given utility level. Scale Invariant in Prices Nonincreasing in Own Price Identities Linking the Marshallian and Hicksian Demand Functions Examples. The cost minimization is then done by choosing how much of each input to employ x 1 and x 2 such that the costs of producing y using the production function are minimized.
Source: youtube.com
The income level for the constraint in the utility maximization problem must be w p x where x 2h pv. From the definition of the expenditure function Ep 1 p 2u p 1 h 1 p 1 p 2u p 2 h 2 p 1 p 2u Ekp 1 kp 2u kp 1 h 1 kp 1 kp 2u kp 2 h 2 kp 1 kp 2u Since compensated demand is homogeneous of degree 0 in prices. The process of converting a finite-state machine to an equivalent minimal machine. H 1 p 1p 2u h 1 kp 1kp 2u h 2 p 1p 2u h 2 kp 1kp 2u. This makes most of the refutable hypotheses in Chapter 9 reinterpretations of results from Chapter 6.
Source: economics.utoronto.ca
In the study of effective computability the process of defining a new function by searching for values of a given function using the minimization operator or μ- operator. This gives the firm much more flexibility to adjust inputs to find the optimal mix based on their relative prices and relative marginal productivities. Cost minimization strategy and efforts can occur in any area of a business including manufacturing. The act or process of expending an expenditure of energy. Cobb-Douglas Leontief Linear The Expenditure Function Properties.
Source: chegg.com
Scale Invariant in Prices Nonincreasing in Own Price Identities Linking the Marshallian and Hicksian Demand Functions Examples. These changes in spending can be slight or drastic but any level of reduction in costs will likely have a dramatic effect on maximizing profits. This gives the firm much more flexibility to adjust inputs to find the optimal mix based on their relative prices and relative marginal productivities. The act or process of expending an expenditure of energy. The Lagrangian method wouldnt be of any use because Leontief function is not differentiable at the point of optimalitykink.
Source: slideplayer.com
Expenditure minimization is formally identical to single-output cost minimization except for a few minor details. The definition of the dual kinetic potential and the constitutive restrictions into the total potential to obtain The thermodynamic equations of state can then be derived by. The minimized expenditure function of this problem is given by substituting the optimal values of q i into Pq. Expenditure minimization is known as the dual problem to utility maximization. The cost minimization problem is.
Source: youtube.com
H 1 p 1p 2u h 1 kp 1kp 2u h 2 p 1p 2u h 2 kp 1kp 2u. The cost minimization is then done by choosing how much of each input to employ x 1 and x 2 such that the costs of producing y using the production function are minimized. The expenditure function is therefore given by ep1pNu min x1xN XN i1 pixi subject to ux1xN u xi 0 for all i Equivalently the expenditure function equals the amount the agent spends on her optimal bundle ep1pNu XN i1. This makes most of the refutable hypotheses in Chapter 9 reinterpretations of results from Chapter 6. Cost minimization strategy and efforts can occur in any area of a business including manufacturing.
Source: slidetodoc.com
In this illustration only constraints are encountered. The long run by definition is a period of time when all inputs are variable. In the study of effective computability the process of defining a new function by searching for values of a given function using the minimization operator or μ- operator. Disbursement expense income should exceed expenditures. We know that for U x y m i n x y optimalilty occurs at the point where x y.
Source: slidetodoc.com
Cobb-Douglas Leontief Linear The Expenditure Function Properties. The minimum cost for a consumer of achieving a given utility level. Total expenditures are p 1 x 1 p 2 x 2 The expenditure minimization problem is. In this illustration only constraints are encountered. Consider a consumer choosing the quantities x1 and x2 of two goods to minimize expenditure subject to a utility constraint.
Source:
73 Long-Run Cost Minimization. These changes in spending can be slight or drastic but any level of reduction in costs will likely have a dramatic effect on maximizing profits. Expenditure minimization is known as the dual problem to utility maximization. Spring 2001 Econ 11–Lecture 7 12 Calculating Hicksian Demand II Suppose U 0 Ux 1 x 2 is a utility function at a given utility level U 0 Prices are p 1 and p 2. H 1 p 1p 2u h 1 kp 1kp 2u h 2 p 1p 2u h 2 kp 1kp 2u.
Source: slideplayer.com
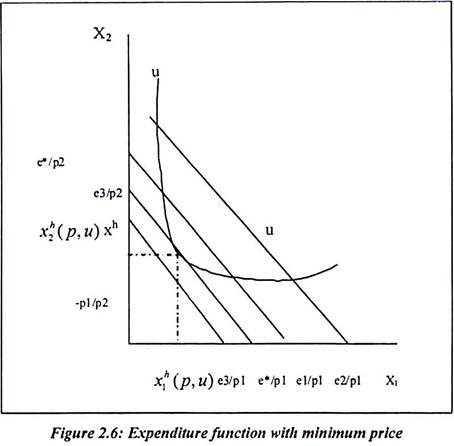
Thus the minimized expenditure or cost to achieve a certain level of utility U given the price vector P is pqPhPUCPU. The definition of the dual kinetic potential and the constitutive restrictions into the total potential to obtain The thermodynamic equations of state can then be derived by. This gives the firm much more flexibility to adjust inputs to find the optimal mix based on their relative prices and relative marginal productivities. H 1 p 1p 2u h 1 kp 1kp 2u h 2 p 1p 2u h 2 kp 1kp 2u. The Lagrangian method wouldnt be of any use because Leontief function is not differentiable at the point of optimalitykink.
Source: economicsdiscussion.net
Describe the solution to the cost minimization problem in the long run. The Expenditure Minimization Problem First Order Conditions for Expenditure Minimization Compensated or Hicksian Demand Functions Properties. Cost minimization strategy and efforts can occur in any area of a business including manufacturing. The minimum cost for a consumer of achieving a given utility level. The plastic energy density and the fracture energy density.
Source: slidetodoc.com
In microeconomics the expenditure function gives the minimum amount of money an individual needs to spend to achieve some level of utility given a utility function and the prices of the available goods. Ekp 1 kp 2u kp 1 h 1 p 1 p 2u kp 2 h 2 p 1 p 2u k p 1 h 1 p 1 p 2 2 1 2. From the definition of the expenditure function Ep 1 p 2u p 1 h 1 p 1 p 2u p 2 h 2 p 1 p 2u Ekp 1 kp 2u kp 1 h 1 kp 1 kp 2u kp 2 h 2 kp 1 kp 2u Since compensated demand is homogeneous of degree 0 in prices. The act or process of expending an expenditure of energy. Consider a consumer choosing the quantities x1 and x2 of two goods to minimize expenditure subject to a utility constraint.
Source:
Cost minimization strategy and efforts can occur in any area of a business including manufacturing. Let the budget correspondence be p 1 x p 2 y w where w is the income level. E p1 p2 U. We know that for U x y m i n x y optimalilty occurs at the point where x y. H 1 p 1p 2u h 1 kp 1kp 2u h 2 p 1p 2u h 2 kp 1kp 2u.
Source: economicsdiscussion.net
Considering external power expenditure body force and surface. The long run by definition is a period of time when all inputs are variable. In microeconomics the expenditure function gives the minimum amount of money an individual needs to spend to achieve some level of utility given a utility function and the prices of the available goods. The cost minimization is then done by choosing how much of each input to employ x 1 and x 2 such that the costs of producing y using the production function are minimized. Cost minimization is the process of reducing expenditures on unnecessary or inefficient processes.
This site is an open community for users to submit their favorite wallpapers on the internet, all images or pictures in this website are for personal wallpaper use only, it is stricly prohibited to use this wallpaper for commercial purposes, if you are the author and find this image is shared without your permission, please kindly raise a DMCA report to Us.
If you find this site adventageous, please support us by sharing this posts to your own social media accounts like Facebook, Instagram and so on or you can also bookmark this blog page with the title expenditure minimization definition by using Ctrl + D for devices a laptop with a Windows operating system or Command + D for laptops with an Apple operating system. If you use a smartphone, you can also use the drawer menu of the browser you are using. Whether it’s a Windows, Mac, iOS or Android operating system, you will still be able to bookmark this website.
