Your Elasticity equations are used for solving images are ready in this website. Elasticity equations are used for solving are a topic that is being searched for and liked by netizens now. You can Find and Download the Elasticity equations are used for solving files here. Get all royalty-free images.
If you’re searching for elasticity equations are used for solving images information linked to the elasticity equations are used for solving topic, you have pay a visit to the right blog. Our website always provides you with suggestions for seeking the highest quality video and picture content, please kindly surf and locate more informative video articles and images that fit your interests.
Elasticity Equations Are Used For Solving. Jeff elasticity microeconomics price elasticity of demand Calculating elasticities is actually very easy. Involves calculating the percentage change of price and quantity with respect to. In order to calculate this we need the beginning and ending price and the beginning. In the formula as mentioned above E is termed as Modulus of Elasticity.
Video Elasticity And Kinematics Nagwa From nagwa.com
In this paper an efficient nontraditional finite element method with nonbody-fitting grids is proposed to solve elasticity equations with sharp-edged interfaces in three dimensions. 15 unknowns and 15 equations 6 strains ε mn 3 equilibrium σ 6 stresses σ mn 6 strain-displacements ε 3 displacements u m 6 stress-strain σ-ε IMPORTANT POINT. We want to solve the time-dependent St Venant-Kirchhoff elasticity equations for the following parameters. Given an initial nite-element mesh and a speci ed boundary displacement we solve. If we focus on an arbitrary small volume of this body and set the mass times the acceleration equal to the sum of the internal and external forces acting on we get. Use the price-demand equation below to determine whether demand is elastic inelastic or has unit elasticity at the indicated values of p.
σ is the Stress and ε denotes strain.
σ is the Stress and ε denotes strain. Elasticity is calculated from the following functional formsY a bXlnY a blnXInY a bXIf this video helps please consider a donation. Elasticity looks at the percentage change in quantity demanded divided by the percentage change in price but which quantity and which price should be the denominator in the percentage calculation. The point elasticity approach and the midpoint or arc elasticity approach. If we focus on an arbitrary small volume of this body and set the mass times the acceleration equal to the sum of the internal and external forces acting on we get. In this paper an efficient nontraditional finite element method with nonbody-fitting grids is proposed to solve elasticity equations with sharp-edged interfaces in three dimensions.
Source: researchgate.net
The equations of linear-elasticity are discretized using a higher-order spatially-continuous nite-element method. σ is the Stress and ε denotes strain. The mass density ρ0 11 g cm3. A method of calculating elasticity between two points. Solutions are known for a few very simple geometries.
Source: educba.com
σ is the Stress and ε denotes strain. In this paper an efficient nontraditional finite element method with nonbody-fitting grids is proposed to solve elasticity equations with sharp-edged interfaces in three dimensions. Involves calculating the percentage change of price and quantity with respect to. The first equation is for the price elasticity of demand. A method of calculating elasticity between two points.
Source: nagwa.com
The first equation is for the price elasticity of demand. 86 General solution to the spherically symmetric linear elasticity problem. We want to solve the time-dependent St Venant-Kirchhoff elasticity equations for the following parameters. Involves calculating the percentage change of price and quantity with respect to. Given an initial nite-element mesh and a speci ed boundary displacement we solve.
Source: sciencedirect.com
The point elasticity approach and the midpoint or arc elasticity approach. The details are left as an exercise. The equations that model displacements in an elastic body such as a metal block can be derived using Newtons second law. The equations of linear-elasticity are discretized using a higher-order spatially-continuous nite-element method. The general problem of 3D elasticity is very di cult to solve analytically in general.
Source: semanticscholar.org
In the formula as mentioned above E is termed as Modulus of Elasticity. Constructing preconditioners for solving the KKT systems that result from discretizing the equations in a mixed formulation have been studied by Klawonn 44 45 and Bramble and Pasciak 46. On the boundary normally either the displacement vector is specified or else an applied external boundary force vector is given. This chapter presents the derivation of elasticity equations. The first equation is for the price elasticity of demand.
Source:
Elasticity is calculated from the following functional formsY a bXlnY a blnXInY a bXIf this video helps please consider a donation. More general can be found using numerical methods such as the finite element method but rubber-like material models pose some special challenges for finite element analysis. On the boundary normally either the displacement vector is specified or else an applied external boundary force vector is given. 86 General solution to the spherically symmetric linear elasticity problem. Up to 10 cash back In this paper a novel Hp-Cloud approximate function with Kronecker delta property named herein as HPCK is utilized in a meshless finite volume method for two-dimensional elasticity problems.
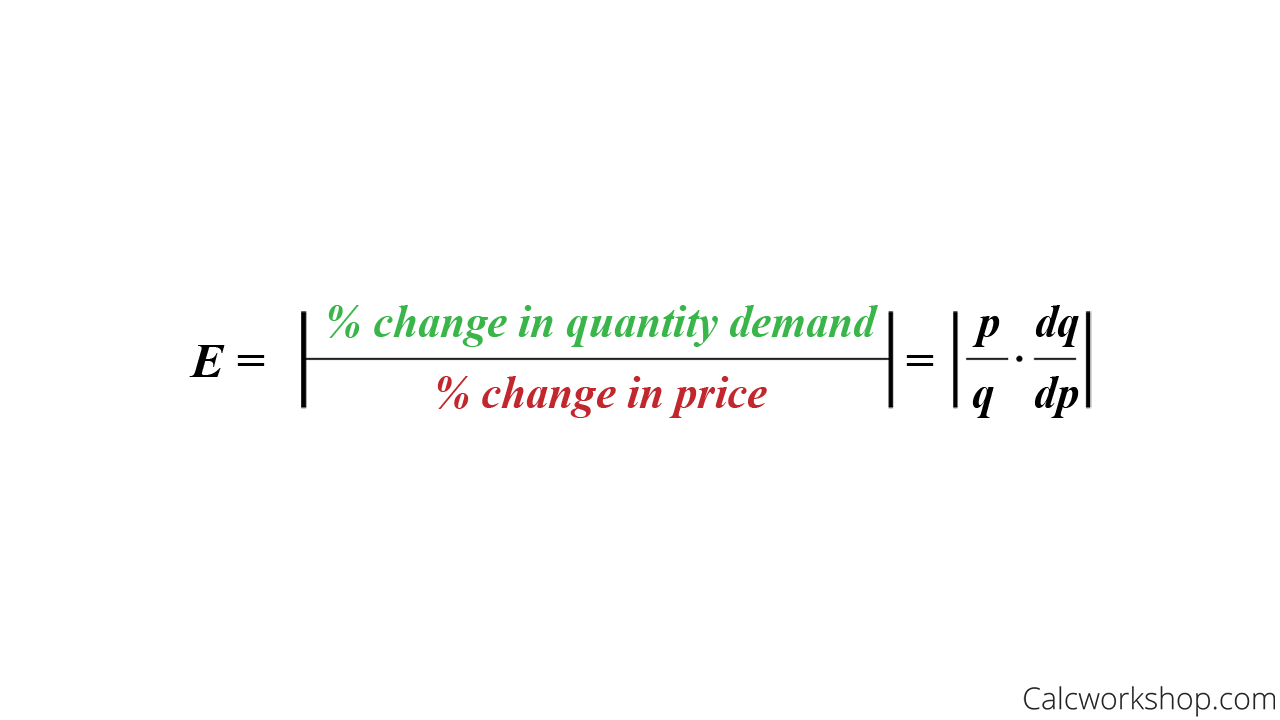Source: calcworkshop.com
Work has also been done on using domain decomposition methods with PCG 47 and GMRES 48 to solve Stokes and elasticity problems. The rst step in trying to tackle the solution of the general elasticity problem is to reduce the system to fewer equations and unknowns by a process of elimination. Elasticity looks at the percentage change in quantity demanded divided by the percentage change in price but which quantity and which price should be the denominator in the percentage calculation. More general can be found using numerical methods such as the finite element method but rubber-like material models pose some special challenges for finite element analysis. In order to calculate this we need the beginning and ending price and the beginning.
Source: researchgate.net
Involves calculating the percentage change of price and quantity with respect to. We can write the expression for Modulus of Elasticity using the above equation as E FL A δL So we can define modulus of Elasticity as the ratio of normal stress to longitudinal strain. The equations of linear-elasticity are discretized using a higher-order spatially-continuous nite-element method. Solving the equation for we see that all other quantities can be found. X fp 1560 - 4p - 01p2 A p 60 B p 80 C p.
Source: reference.wolfram.com
Up to 10 cash back In this paper a novel Hp-Cloud approximate function with Kronecker delta property named herein as HPCK is utilized in a meshless finite volume method for two-dimensional elasticity problems. In this paper an efficient nontraditional finite element method with nonbody-fitting grids is proposed to solve elasticity equations with sharp-edged interfaces in three dimensions. The details are left as an exercise. Given an initial nite-element mesh and a speci ed boundary displacement we solve. The mass density ρ0 11 g cm3.
Source: khanacademy.org
Up to 10 cash back In this paper a novel Hp-Cloud approximate function with Kronecker delta property named herein as HPCK is utilized in a meshless finite volume method for two-dimensional elasticity problems. Must solve for reactions simultaneously with stresses strains etc. Involves calculating the percentage change of price and quantity with respect to. The rst step in trying to tackle the solution of the general elasticity problem is to reduce the system to fewer equations and unknowns by a process of elimination. Chapter 6a Plane StressStrain Equations Learning Objectives To review basic concepts of plane stress and plane strain.
Source: researchgate.net
To derive the constant-strain triangle CST element stiffness matrix and equations. Price Elasticity of Supply SS PP Relevance and Uses of Price Elasticity of Supply Formula From the point of view of a production manager it is very important to understand the concept of price elasticity of supply because it governs the dynamics between the price of a good and the suppliers willingness to supply at that price. These results can be derived as a special case of the general 3D equations of linear elasticity in spherical coordinates. The point elasticity approach and the midpoint or arc elasticity approach. This chapter presents the derivation of elasticity equations.
Source: sciencedirect.com
15 unknowns and 15 equations 6 strains ε mn 3 equilibrium σ 6 stresses σ mn 6 strain-displacements ε 3 displacements u m 6 stress-strain σ-ε IMPORTANT POINT. We want to solve the time-dependent St Venant-Kirchhoff elasticity equations for the following parameters. Our goal is to solve the equations given in Section 85 for the displacement strain and stress in the sphere. On the boundary normally either the displacement vector is specified or else an applied external boundary force vector is given. E is the modulus of elasticity and is Poissons ratio.
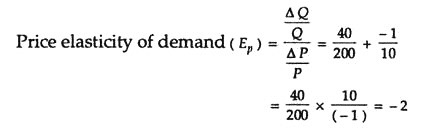Source: economicsdiscussion.net
Depending on the primary unknown of the resulting equations we have the. The equations governing large deformation of elastic solids are nonlinear and are impossible to solve analytically in general. The equations of linear-elasticity are discretized using a higher-order spatially-continuous nite-element method. 15 unknowns and 15 equations 6 strains ε mn 3 equilibrium σ 6 stresses σ mn 6 strain-displacements ε 3 displacements u m 6 stress-strain σ-ε IMPORTANT POINT. σ is the Stress and ε denotes strain.
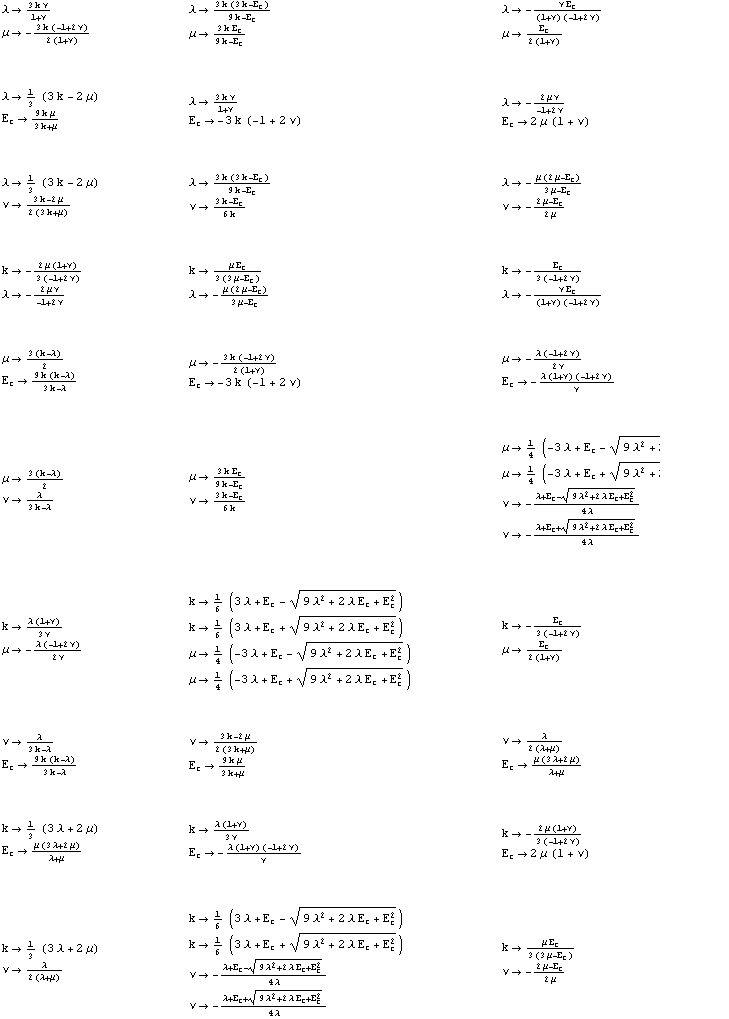Source: reference.wolfram.com
Use the price-demand equation below to determine whether demand is elastic inelastic or has unit elasticity at the indicated values of p. How to solve elasticities problems in economics. A method of calculating elasticity between two points. Involves calculating the percentage change of price and quantity with respect to. In the formula as mentioned above E is termed as Modulus of Elasticity.
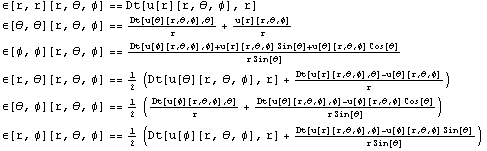Source: reference.wolfram.com
The equations of linear-elasticity are discretized using a higher-order spatially-continuous nite-element method. More general can be found using numerical methods such as the finite element method but rubber-like material models pose some special challenges for finite element analysis. Up to 5 cash back The equations that model displacements in an elastic body such as a metal block can be derived using Newtons second law. We want to solve the time-dependent St Venant-Kirchhoff elasticity equations for the following parameters. S is found in Table 3 and is The radius is 0750 mm as seen in the figure so the cross-sectional area is The value for is also shown in the figure.
Source: sciencedirect.com
15 unknowns and 15 equations 6 strains ε mn 3 equilibrium σ 6 stresses σ mn 6 strain-displacements ε 3 displacements u m 6 stress-strain σ-ε IMPORTANT POINT. Constructing preconditioners for solving the KKT systems that result from discretizing the equations in a mixed formulation have been studied by Klawonn 44 45 and Bramble and Pasciak 46. Solving the equation for we see that all other quantities can be found. A method of calculating elasticity between two points. We can write the expression for Modulus of Elasticity using the above equation as E FL A δL So we can define modulus of Elasticity as the ratio of normal stress to longitudinal strain.
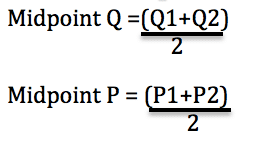Source: economicshelp.org
We can write the expression for Modulus of Elasticity using the above equation as E FL A δL So we can define modulus of Elasticity as the ratio of normal stress to longitudinal strain. We can write the expression for Modulus of Elasticity using the above equation as E FL A δL So we can define modulus of Elasticity as the ratio of normal stress to longitudinal strain. Epo variation of Qo Qo variation of P P ΔQ or Q o ΔP P Then the value assumed by the price elasticity of supply indicates the percentage in which the quantity offered changes from 1 in the price. In this case you must employ the stress-strain equations – Overall this yields for elasticity. The equations that model displacements in an elastic body such as a metal block can be derived using Newtons second law.
Source: sciencedirect.com
Chapter 6a Plane StressStrain Equations Learning Objectives To review basic concepts of plane stress and plane strain. The details are left as an exercise. Elasticity is calculated from the following functional formsY a bXlnY a blnXInY a bXIf this video helps please consider a donation. The equations that model displacements in an elastic body such as a metal block can be derived using Newtons second law. Solutions are known for a few very simple geometries.
This site is an open community for users to share their favorite wallpapers on the internet, all images or pictures in this website are for personal wallpaper use only, it is stricly prohibited to use this wallpaper for commercial purposes, if you are the author and find this image is shared without your permission, please kindly raise a DMCA report to Us.
If you find this site serviceableness, please support us by sharing this posts to your favorite social media accounts like Facebook, Instagram and so on or you can also save this blog page with the title elasticity equations are used for solving by using Ctrl + D for devices a laptop with a Windows operating system or Command + D for laptops with an Apple operating system. If you use a smartphone, you can also use the drawer menu of the browser you are using. Whether it’s a Windows, Mac, iOS or Android operating system, you will still be able to bookmark this website.
